LRU算法建模
什么是LRU(Least-Recently Used)
-
缓存的队列长度(容量)为\(S\), 一共有\(K\)的项, K » S > 0。
-
每一个缓存项被访问的概率为\(\alpha_k\), \(k\subseteq(1, K)\)
-
当某个缓存项被命中后,它会被移到缓存的第一位。如果某项没有被命中,会被存入第一位,此时,如果缓存队列容量大于\(S\),最末尾的缓存项会被移除缓存队列。
King,Flagolet 模型公式
最早提出计算LRU未命中的概率计算是由W.F.King提出的计算公式: \(s\) 为cache的容量。每一项为\(p_i,i\in[1..K], \sum_{i=1}^Kp_{i}=1\)
\[P_{miss} = \sum_{s-tuple\{i_1,i_2,\dots,i_s\}\\ i_1\neq i_2\neq i_3 \neq \dotsc \neq i_s} p_{i_1}\frac{p_{i_2}}{1 - p_{i_1}}\frac{p_{i_3}}{1-p_{i_1}-p_{i_2}}\dotsc\frac{p_{i_s}}{1-p_{i_1}-p_{i_2}-\dotsc p_{i_{s-1}}}(1-p_{i_1}-p_{i_2}-\dotsc p_{i_s})\]这个公式倒是比较好理解,不过计算起来比较麻烦,\(s-tuple\)为\(p_i,i\in[1..K]\)的排列\(A_{K}^S\)
Flajolet等人在92年一片论文(Birthday paradox, coupon collectors, caching algorithms and self-organizing search)中论证了
\[1 - P_{miss} = \sum_{q=0}^{s-1}[u^q]\int_0^\infty (\prod_{i=1}^s(1+u(e^{p_{i}t} - 1)))(\sum_{i=1}^m{\frac{p^2_i}{1+u(e^{p_{i}t }-1)}})e^{-t}\mathrm{d}x\]推倒中用到了生成函数和Laplace-Borel transform,这个公式其实我没太看懂。
在Identity of King and Flajolet & al. Formulae for LRU Miss Rate Exact Computation论文中,作者Christian Berthet证明了King与Flajolet两个公式为等价的。
马尔可夫过程模型
这个方法借鉴了Modeling Hierarchical Caches in Content-Centric Networks这片论文中模型的设计方法。
用Markov chain建模计算LRU命中率的方法,相比于King的方法将时间空间由指数降为了平方阶。
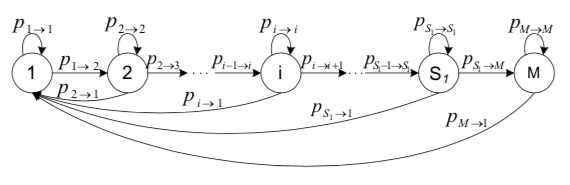
在此图中,
一共有\(M = S + 1\)个状态,其中状态\(M\)为miss,即未在队列。 \(P_{i,j}\) 为一次访问后状态从状态\(p_i\)到\(p_j\)。一共有四种转换的情况
- \(P_{i,i}, i\subseteq[2, S]\),在一次访问后,其队列的位置没有发生变化
- \(P_{M,M}\), 在一次访问中,其还出为未被缓存的状态
- \(P_{i-1, i}, i\subseteq[2, M]\), 在一次访问中,其队列位置向后一位
- \(P_{i,1}, i\subseteq[1, M]\), 在一次访问中,被命中,被移动到队列的第一位
设缓存项\(k\),在\(p_i\)状态的概率为\(p_k(i)\), \(b_k = \sum_{t=1}^{k}p_k(t)\)
\[P_{i,i} = \sum_{t=1}^{K}\alpha_tb_t(i-1)\] \[P_{M,M} = 1 - \alpha_k\] \[P_{i-1,i} = 1 - \sum_{t=1}^{K}\alpha_tb_t(t-2) - \alpha_k\] \[P_{i,1} = \alpha_k\]根据这些转移概率,可以写出其平衡方程组: \(\begin{cases} \pi_1 &= \alpha_k\sum_{i=1}^{K}\pi_i&\\ \pi_i & = P_{i,i}\pi_i + P_{i-1,i}\pi_{i-1}& {i \subseteq[2,M]} \end{cases}\)
\(p_k(i) = \pi_i\),那么\(p_k(i)\)的递归求解公式为:
\[p_k(i) = p_k(i-1)\frac{1-\sum_{t=1}^{K}\alpha_tb_t(i-2)-\alpha_k}{1- \sum_{t=1}^{K}\alpha_tb_t(i-1)},i\subseteq[2,M]\]其中\(p_k(1)=\alpha_k\)
这样以来,项\(k\)的命中率\(h_k=\sum_{i=1}^{S}p_k(i)\),整体LRU在稳定状态下的命中率即为: \(H=\sum_{k = 1}^{K}\alpha_kh_k\)
下面是用计算机模拟生成数据和使用马尔可夫模型推倒的公式的对比。数据是生产中遇到的数据。
- 请求服务的key中500个头部key占总请求的50%
- 请求服务的key中3500个中部key占总请求的35%
- 请求服务的key中100000个尾部key占总请求的15%
下图可以看到,在模拟按概率请求的结果与公式推倒的结果是吻合的。
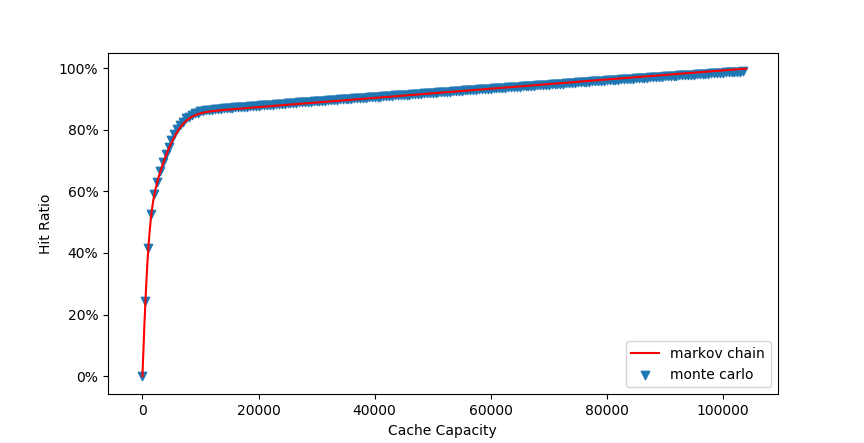
从结果也可以看出,在刚开始增大cache的容积,对命中率有显著地提升。命中率趋势有点像指数级增长。在超过80%以后,由于是概率比较小的长尾key的影响,失去了空间局部性,提升基本就是线性的了,增加cahce容积获得命中率提升性价比比较低。
19 Dec 2019 by John Brown